Is a frisbee flip fair?
Spoiler: it’s definitely not. To see why, watch this short video, and read the explanation below.
Introduction
In the exceptionally athletic sport of ultimate frisbee, the starting positions of the teams are often decided by a simple probability game. In this game, the captains of each team both toss a frisbee in the air with lots of vertical rotation. One of the captains will call ‘evens’ or ‘odds’ which refers to the orientation of the discs when they land on the ground.
In highly competitive ultimate frisbee games, winning this initial disc flip can provide an advantage to the victorious team. However, this game is probabilistically unfair. Using a combination of real trials and mathematical techniques, we will explore exactly why this game is unfair, as well as review a potential solution.
Background
A single frisbee can land ‘heads’ or ‘tails.’ ‘Heads’ refers to when the decorative side of the disc is facing up. ‘Tails’ refers to when the inside of the disc is facing up (the decorative side of the disc is facing down). Figure 1 depicts this clarification:

Figure 1: Left ‘heads’, right ‘tails’
In the double-disc flip, two frisbees are thrown and the orientation is called as ‘evens’ or ‘odds.’ ‘Evens’ refers to when the two frisbees are either both ‘heads’ or both ‘tails.’ ‘Odds’ refers to when one frisbee is heads and one frisbee is tails. In Figure 1 above, this combination would be ‘odds.’ The double-disc flip technique is utilized in an attempt to reduce any bias there may be for a frisbee to physically land ‘heads’ or ‘tails.’ However, this is still not a fair game. To see this, we will build intuition by starting with a single frisbee.
Single Disc Flip
To gather data, a single sanctioned ultimate frisbee disc was flipped a total of 250 times, in the same environment. The result was 136 heads and 114 tails. With this dataset, that’s about a 54% chance it lands heads and a 46% chance it lands tails.
However, in the real world, ultimate frisbee is played on a variety of fields, in different conditions, with all kinds of frisbees (that meet the material and weight requirements). Rain, wind, grass, turf, and we’ve all come across a field with a dirt patch or two. All of these factors have an impact on a way a disc flips, so we continued to collect data on both grass and on turf, in a variety of weather conditions, with different discs and different people. With this dataset, we had 650 flips, 341 heads and 304 tails. That’s a 52.5% chance of heads and a 47.5% chance of tails.
In a perfect probabilistic world, all of the discs and environments would act the same. But we all know that this isn’t the case. Every disc and every field is different, which means that every disc has a different probability of landing ‘heads.’ We can calculate this value more precisely using different probability concepts.
Consider the disc used for the original 250 flips. We model the probability of a disc landing heads as a Beta random variable. As we gather data, we update our distribution accordingly. To estimate the sampling distribution of this statistic, we utilize a method called bootstrapping which resamples the dataset. Coding this in python, we found if X ~ Beta(, ), with 100,000 trials, = 54125 and = 46125.
We can see from Figure 2 and Figure 3 that the probability distribution changes after the bootstrapping technique, as does the precision of the probabilities.
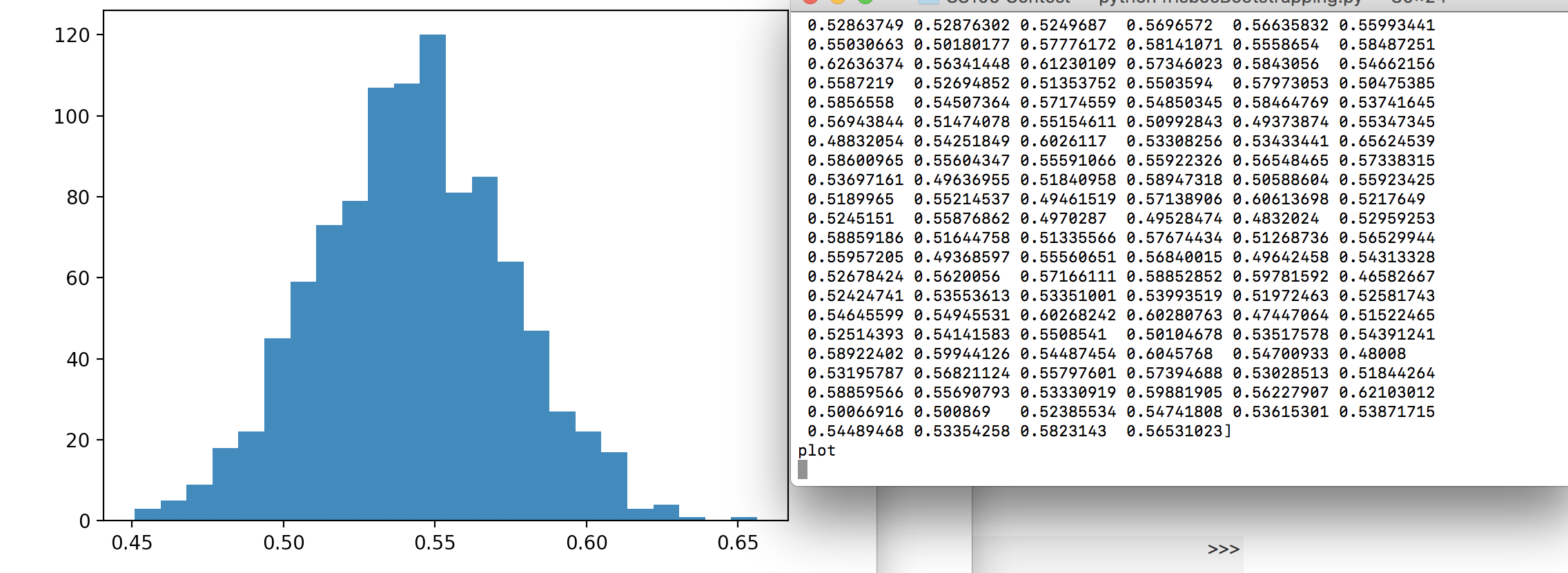
Figure 2: Before bootstrapping technique
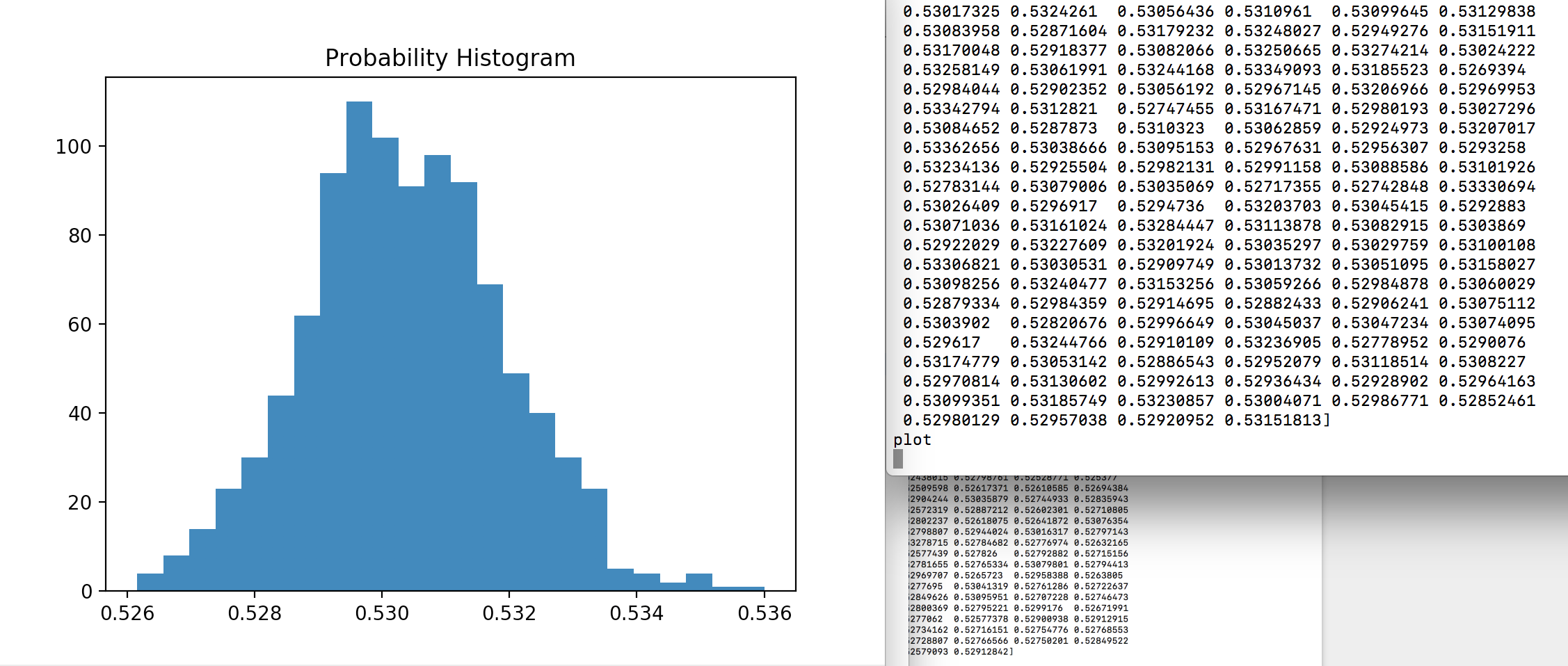
Figure 3: After bootstrapping technique
More precisely, a mathematical representation of the Beta PDF with the original and from the single disc data gives us Figure 4.
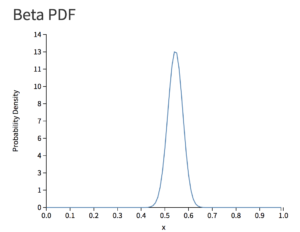
Figure 4: This was generated using the Beta tool from the Stanford CS109 website
Calculating the expectation of the Beta would give us a p-value for this particular disc landing heads:
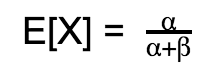
Which comes out to be 0.5399.Thus, this particular frisbee has about a 53.99% chance of landing heads in this environment, when I am flipping the disc.
Double Disc Flip
To reduce this bias, the double-disc flip is utilized to start ultimate frisbee games. This method is supposed to guarantee than an odd combination of disc results is never more probable than an even result. However, it still isn’t a fair game.
Mathematically, assuming that each flip is an independent event, we can multiply the events together to calculate the probability of each possible combination of disc orientations. Consider the single-disc example from before.
We sum the events that we have defined as ‘evens’ and ‘odds’ to attain the final probability of the flips: Evens = TT + HH = 0.5032, Odds = TH + HT = 0.4968. This method does minimize the bias compared to the single-disc case. However, even with this slight difference, we can still expect for every 200 games, which is approximately how many total games are played at USAU Nationals, that at least one toss will go the way of a team.
So… how do we achieve a fair game without losing the ultimate frisbee flavor?
Fair Game Proposal
To solve this, I present a slight variation on the two-disc flip method. Here is the proposed strategy:
- Both captains flip a frisbee that they provide
- If both discs land in the same orientation (‘Evens’: either both ‘heads’ or both ‘tails’), the captains reflip
- If both discs land in different orientations, the captain with the ‘heads’ orientation wins
Let p = the probability that the frisbee lands with the ‘heads’ orientation. For the purposes of this analysis, we assume that p is the same for both frisbees.
We calculate the probabilities of each team winning on a given flip:
Probability of team A winning = p(1-p)
Probability of team B winning = (1-p)p
Since there is a re-flip involved, there is also the possibility that the captains flip infinitely.
Probability of not finishing = 1-2p(1-p)
The probabilities of each captain winning can be modeled by an Infinite Geometric Sum:
Probability of team A winning = i=0(1-2p(1-p))i*p(1-p) =1/2
Probability of team B winning = i=0(1-2p(1-p))i*(1-p)p =1/2
Expected number of flips before winner is decided = i=0(1-2p(1-p))i*2p(1-p)*(i+1)
For example, if p = 0.50, then 1 flip is expected half of the time, 2 flips one-fourth of the time, and so on. The infinite sum n/2^n is 2, so we expect roughly 2 flips on average to be the number of iterations it takes to determine the winner (50% of the time it will be even fewer, and 75% of the time it will be 2 or less).
This strategy is an excellent alternative to the current method, as it requires the same amount of effort, and ensures a fair game.
Further Exploration
There were multiple interesting factors that we did not examine in this project.
One is every individual’s flipping technique. When flipping a frisbee, the thrower’s motion certainly has an effect on which orientation the disc is likely to land. This means that, potentially, we could calculate every player’s p-value of flipping a frisbee heads. By flipping a variety of discs in multiple environments, Superfly (Stanford Women’s Ultimate A team) could determine which captain is most likely to flip ‘heads,’ and have them always flip during a game.
Another factor is the actual disc. As mentioned before, every disc likely has a different p-value. The discs used during frisbee games are regulated to be a certain size, make, and weight. But it’s impossible to control every curvature or slight bend of each individual disc. Thus, we could see just how much variation there is between discs, by trying these techniques on dozens of frisbees.
Lastly, I would like to explore the actual impact of this disc flip. Is the team that wins the flip more likely to win? Typically, the flip has very little impact on the outcome of the game. But in some highly competitive ultimate games, the scores are so close that it could end up being the difference. Unfortunately, the winner of the flip is not typically recorded for every game, so it is a difficult to evaluate without a lot of real data.
Conclusion and Further Reading
Ultimate frisbee is a wonderful game with a heavy emphasis on ‘spirit of the game’ (good sportsmanship), athleticism, and teamwork. It is rapidly growing in popularity, and will continue to be a large part of many people’s lives, all around the world.
You can find the Stanford Women’s Ultimate website here: http://ultimate.stanford.edu/
The official ultimate frisbee rules can be viewed here: https://www.usaultimate.org/resources/officiating/rules/11th_edition_rules.aspx
For some interesting discussion about the probability of a frisbee flip, check out this Reddit post and SKYD magazine article:
https://www.reddit.com/r/ultimate/comments/slrs1/frisbee_flipping_statisticsprobability/
https://skydmagazine.com/2011/02/heads-tails/
Download a copy of the write-up of the project here.
